Bővebben a munkabizonyítékról

Szerző: Amir Taaki

A Bitcoin rendszerének egyik alapját a munkabizonyíték-algoritmus adja. Ez egy olyan, számítási úton megoldandó probléma, amelynek a megoldásával bizonyítod azt, hogy valóban szorgosan munkálkodtál a megoldásán. A Bitcoin kontextusában a munka az áramfelhasználásra utal, a bizonyíték pedig a “célellenőrzésre”.

Hashelés

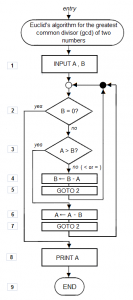
A tényleges algoritmus egy hashfunkciót tartalmaz. Egy algoritmus pedig nem más, mint egy probléma megoldásának menetét tartalmazó utasítássorozat. Algoritmus például egy számítógépes program működési elvét szemléltető absztrakt folyamatábra is.

Az algoritmusokat aztán afféle feketedobozokba, úgynevezett funkciókba rakhatjuk. A funkció lényege abban áll, hogy különböző adatokat fogad a bemeneténél, elvégzi velük/rajtuk a feladatát, majd attól függően, hogy pontosan miben is állt ez a feladat, kiadja a megfelelő eredményeket a kimenetnél.

Amikor tehát a programozók algoritmusokat emlegetnek, akkor ilyesféle utasítássorozatokra vagy folyamatokra gondolnak, és azoknak is konkrétan a belső részleteire, működési elvére. Ha pedig funkciók kerülnek szóba, akkor inkább az eredményekre kíváncsiak, semmint az azt előállító folyamat technikai finomságaira. Jelen cikkben is azért említünk tehát munkabizonyíték-algoritmust, mert annak a belső mechanizmusairól beszélünk. Míg ezzel szemben a munkabizonyíték-algoritmus által alkalmazott hashfunkció részleteire annyira nem vagyunk kíváncsiak, de annál inkább az általa előállított eredményekre, és annak a munkabizonyíték-algoritmusban játszott szerepére.

A hashfunkció lényege, hogy egy bemeneti adatot egy olyan kimeneti adattá konvertál, amelyek között gyakorlatilag lehetetlen bármiféle kapcsolatot is felfedezni. Az igazán jó hashfunkciók (számos különböző féle és fajta létezik az MD5-től az SHA-ig) szinte soha nem generálnak ütközést – vagyis olyan esetet, amikor két, egyébként teljesen különböző és egymással össze nem függő bemeneti értékből mégis pontosan ugyanazt a kimeneti értéket állítják elő.

kulcsok / hashfunkció / hashek

A gyakorlatban ez azt jelenti, hogy a hashfunkciók sokszámjegyű hash-értékeket generálnak.

$ python
>>> import hashlib
>>> hashlib.sha256("hello").hexdigest()
'2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824'


A “hello” kifejezést adtuk meg tehát az SHA256 hashfunkciónak, amiből annak az algoritmusa a fent (és itt is) látható hash-értéket állította elő:

2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824

A jó hashfunkció további ismérve, hogy a bemeneti adatok már egészen csekély mértékű módosítása is óriási különbségeket eredményez a kimeneti értékben; így ugyanis rendkívül nehéz (gyakorlatilag lehetetlen) visszafejteni a bemeneti értéket a kimenetiből – míg ellenben a gyenge hashfunkcióknál (elegendő számítókapacitás birtokában) ez már korántsem olyan nagy kihívás. Ha például túl kevés számból áll a kimeneti érték és nem is túl nagy a variancia, akkor lehet érdemi esély a visszafejtésre. De ugyanígy gondot okoz az is, ha túl sok ütközést generál a funkció.

A kiinduló feltételek csekély változásai is jelentős, nehezen visszafejthető változásokhoz vezetnek a kimeneti értékekben.

Egy egyszerű, de annál hatékonyabb biztonsági intézkedés például az, ha egy weboldal a regisztrált felhasználóinak a regisztráláskor megadott jelszavát nem tárolja el sehol, csak a jelszó hashét. Valahányszor a felhasználó szeretne bejelentkezni, az oldal gyorsan lehasheli a megadott jelszót, összeveti az eredményt az adatbázisában tárolt hash-értékkel, és ha a kettő megegyezik, akkor nyugodtan beengedheti az illetőt. Ez semmiféle fennakadást nem okoz a rendszer működésében, viszont garantálja a felhasználók biztonságát, mivel még ha egy támadó sikeresen fel is törné az oldal szerverét és ellopná a felhasználók adatbázisát, akkor sem ismerhetné meg a jelszavaiakat, és nem férhetne hozzá a fiókjaikhoz. Minden weboldalnak ezt a módszert kellene használnia – valamilyen erős hashfunkcióval.

Ez volt a baj annak idején, az MtGox nevezetes feltörésekor is: hogy bár ők is csak hashértékeket tároltak el jelszavak helyett, de gyenge hashfunkciót használtak. A támadó így könnyen végigpörgethette a gépén a különböző kombinációkat, reprodukálhatta a hash-értékeket és számos felhasználó jelszavát deríthette ki. Egy jó hashfunkció azonban kivitelezhetetlenné (vagy legalábbis nagyon nem praktikussá) teheti ezt a fajta támadást.

Munkabizonyíték

A Bitcoin munkabizonyíték-algoritmusa igen egyszerű:

1.) Aktuális blokk lehashelése.
2.) Célszám kiszámítása az aktuális nehézség alapján.
3.) Alacsonyabb lett a blokk hashértéke a kiszámított célszámnál?

A bitcoin-bányászok mindaddig folyamatosan hashelik az éppen soron lévő blokkjukat, amíg igennel nem tudnak felelni a harmadik pontban megfogalmazott kérdésre. Nemleges válasz esetén ejtenek egy apró módosítást a blokkon, kezdik előről, és folytatják ezt a folyamatot így mindaddig, amíg nem kapnak egy megfelelő eredményt. Ha pedig megvan az eredmény, akkor azonnal szétküldik a hálózatba a sikeresen lehashelt blokkot.

A nehézséget mindig a hálózat határozza meg; nagyjából kéthetente vizsgálja meg, hogy indokolt-e az újrabeállítás, és ha igen, akkor a szükséges mértékben korrigálja az értéket. Ha eddig túl nehéz volt a bányászat, akkor könnyít rajta, ha túl könnyű, akkor nehezít.

Ezért kezdődnek a Bitcoin-blokkok hashei egy sor nullával. Az 163701. blokk hash-értékének a hexadecimális alakja például így néz ki:

00000000000009611e31fd14c3c786bb792e17f9b95f65620491ac55ed4bc018

Tizes számrendszerben ez ennyit jelent:

15072061652479515824586354748403488046119941424972330391289880

Aztán, ha jobban megnézzük a 163701. blokkot, úgy láthatunk ott egy olyan mezőt is, hogy “Bits”:

Difficulty: 1307728.360604 (“Bits”: 1a0cd43f)

A Bits értékéből a következő képlettel számíthatjuk ki a célszámot:

t = b2 · 28(b1 - 3)

A b₁ a “Bits” értékünk első bájtja; 0x1a hexadecimálisan (26 tizes számrendszerben), a b₂ pedig az érték maradéka, vagyis 0x0cd43f (840767).

t = 0x0cd43f · 28(0x1a - 3)

>>> 0x0cd43f * 2**(8*(0x1a - 3))
20615546854515052444405957679617344022137222968655050411343872L
>>> "%x"%(0x0cd43f * 2**(8*(0x1a - 3)))
'cd43f0000000000000000000000000000000000000000000000'

A célszám lehetséges maximumát a 0x1d00ffff állandó határozza mg.

>>> "%x"%(0x00ffff * 2**(8*(0x1d - 3)))
'ffff0000000000000000000000000000000000000000000000000000'

A nehézséget a következőképpen határozzuk meg:

nehézség = a célszám lehetséges maximuma / a célszám jelenlegi egyezményes értéke

A példánknál maradva:

>>> 0xffff0000000000000000000000000000000000000000000000000000 / float(0xcd43f0000000000000000000000000000000000000000000000)
1307728.3606040676

Ami pontosan megegyezik a Block Exploreren korábban is megfigyelt nehézséggel. Így most már ismerjük tehát a jelenlegi célszámot, és megvan a blokk hashe is. Ha a blokk érvényes és megfelel a munkabizonyíték-teszten, akkor az azt jelenti, hogy a hash-értéke valóban alacsonyabb a jelenlegi célszámnál.

0x00000000000009611e31fd14c3c786bb792e17f9b95f65620491ac55ed4bc018 < 0xcd43f0000000000000000000000000000000000000000000000

Igaz

A bányász feladata tehát a blokk mindaddig való módosítása, amíg a módosítás következtében olyan hash-értéket nem kap hozzá, amelyik megfelel a fenti teszten. A példablokkunknál maradva, láthatunk ott egy bizonyos “Nonce” nevezetű mezőt is.

Nonce: 2528486661

A blokkok módosítása pedig egész pontosan ennek a “nonce”-értéknek az egyesével való növelését jelenti: növelik az értéket, újrahashelik a blokkot, ellenőrzik az eredményt, és ha nem jó, újra növelik, újra hashelik, és így tovább. Megtehetik azonban azt is, hogy teljesen véletlen nonce-értékeket generáltatnak a géppel, vagy hogy más módon, például a tranzakciók sorrendjének átrendezésével módosítják a blokkot. Ha pedig a nonce eléri a maximális értékét, akkor a blokk legelső tranzakcióját módosítják, és úgy dolgoznak tovább (vagyis az ún. “coinbase nonce”-ot növelik, avagy IncrementExtraNonce(...)).

Nem egyszerű létrehozni egy blokkot, lévén ez a folyamat igen sok számítókapacitást igényel, ebből következően tehát sok áramot, és ebből következően sok pénzt is. A bányászat nyeresége minimális, rosszabb esetben még veszteséges is lehet. Minél többen bányásznak, annál magasabbra emeli a hálózat a nehézséget, és ezzel arányosan csökken a bányászat nyereségessége is.

Amikor pedig valaki sikeresen létrehoz egy olyan blokkot, ami megfelel a munkabizonyíték-teszten, nyomban körbeküldi azt a hálózatban, hogy a többiek is ellenőrizhessék, majd beépíthessék a saját blokkláncukba és abból kiindulva kezdhessenek dolgozni a következő blokkon.

Andrew Bitcoiner kommentje: Méretét tekintve mekkora a hashelt blokk?

Amir Taaki válasza: Mindig 80 bájt. Ezt azért alakították így, hogy nyugodtan felvehessenek bele bármennyi tranzakciót a bányászok.

http://gitorious.org/libbitcoin/libbitcoin/blobs/master/include/bitcoin/messages.hpp

struct block
{
uint32_t version;
hash_digest previous_block_hash;
hash_digest merkle;
uint32_t timestamp;
uint32_t bits;
uint32_t nonce;
transaction_list transactions;
};

http://gitorious.org/libbitcoin/libbitcoin/blobs/master/src/block.cpp

{
serializer key;
key.write_4_bytes(block.version);
key.write_hash(block.previous_block_hash);
key.write_hash(block.merkle);
key.write_4_bytes(block.timestamp);
key.write_4_bytes(block.bits);
key.write_4_bytes(block.nonce);
return generate_sha256_hash(key.data());
}

Forrás: Bitcoin Media

A lap szövege Creative Commons Nevezd meg! – Ne add el! – Így add tovább! 3.0 licenc alatt áll, felhasználni csak forrásmegjelöléssel, és ide mutató linkkel szabad.