Bitcoin:
A P2P-alapú elektronikus pénz rendszere

Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org

Kivonat. Egy tisztán P2P-alapú elektronikus pénzrendszerrel az érintett felek közvetítő pénzintézetek nélkül, közvetlenül egymás között bonyolíthatnák le az online fizetéseket. A megoldás részét képezik a digitális aláírások is, de teljes csak akkor lehet a rendszer, ha meg tudja akadályozni egyazon összegek többszöri elköltését. A felvázolt P2P-rendszer pontosan erre a problémára nyújt megoldást. A hálózat a tranzakciók hashelésével és egybefüggő, hash-alapú munkabizonyíték-láncba fonásával időbélyegzi a tranzakciókat. A tranzakció-bejegyzések ily módon létrehozott láncolatát így utólag már nem lehet megváltoztatni a munkabizonyítékok újraszámítása nélkül. A leghosszabb lánc nem csak a benne foglalt események valódiságát és rögzített sorrendiségét tanúsítja, hanem egyben azt is, hogy a hálózat legnagyobb számítókapacitás-tömörülése hozta létre. Mindaddig, amíg a hálózat számítókapacitásának többsége nem áll egy esetleges támadó szervezett irányítása alatt, a szabad csomópontok által vezetett és bővített lánc mindig hosszabb lesz és gyorsabban is fog bővülni, mint a támadóé. Maga a hálózat minimális szervezést igényel. Az üzenetek best effort-alapon kerülnek továbbításra, a csomópontok pedig tetszés szerint hagyhatják el a hálózatot vagy térhetnek vissza, elfogadva a leghosszabb munkabizonyíték-láncot a távollétük alatt lezajlott események bizonyítékaként.

1. Bevezető

Az internetes kereskedelem mára szinte teljes egészében az elektronikus fizetéseket bizalmas harmadik félként kezelő pénzintézetek szolgáltatásai köré fonódott. És bár ez a rendszer a legtöbb tranzakció esetében valóban elég jól működik, a bizalom-alapú modell természetéből fakadó gyengéin nem tud felülkerekedni. Nem igazán lehetségesek például 100%-ban visszafordíthatatlan tranzakciók, mivel a pénzintézetek nem kerülhetik el az utalásokkal és a pénz kezelésével kapcsolatos vitákat. Közvetítői költségek rakódnak a tranzakciókra, kialakítva így a még praktikusnak mondható tranzakciók minimális alsó értékhatárát és ellehetetlenítve az alkalmi, kis összegű tranzakciókat. Veszteségként könyvelhetjük el továbbá a vissza nem fordítható szolgáltatásokért adható vissza nem fordítható fizetés lehetőségének hiányát is. A visszafordíthatóság lehetősége csak fokozza a bizalom iránti igényt; a kereskedőket gyanakvásra készteti a vásárlókkal szemben, valamint tőlük a feltétlenül szükségesnél több adat és információ kicsikarására. És még így is bele kell törődnünk egy bizonyos százaléknyi elkerülhetetlen csalási arányba. Élőben, készpénz használatával elkerülhetőek ugyan ezek a költségek és fizetési bizonytalanságok, de egy kommunikációs csatornán keresztüli fizetés lebonyolítására nincs mód bizalmas harmadik fél nélkül.

Ezért van szükség tehát egy olyan elektronikus fizetőrendszerre, ami nem bizalomra, hanem kriptográfiai bizonyítékokra épül; melynek segítségével a felek anélkül bonyolíthatják le közvetlenül egymás között a fizetéseiket, hogy ehhez egy bizalmas harmadik fél szolgáltatásait kellene igénybe venniük. Az olyan tranzakciók, melyeknek a visszafordítása aránytalanul nagy számítókapacitást igényelne, az eladókat is védik a csalóktól, rutinszerű zálogmechanizmusok beépítésével pedig a vásárlók is könnyen védhetőek. Jelen dolgozatban egy P2P-alapú, elosztott időbélyegző szerverre épülő megoldást kínálunk a többszöri elköltés problémájára. Ez a szerver számítási bizonyítékok generálásával tanúsíthatja a tranzakciók időbeli sorrendjét. A rendszer mindaddig teljesen biztonságos, amíg abban a tisztességes csomópontok összesen nagyobb számítókapacitást képviselnek, mint bármely támadó saját irányítása alá vont, összehangoltan dolgozó csomópontjai.

2. Tranzakciók

Egy elektronikus érmét digitális aláírások láncolataként határozunk meg. Ezt az érmét a tulajdonosa úgy adhatja át valaki másnak, ha digitálisan aláírja egyrészt az előző tranzakció hashét (melynek révén az érme hozzá került), másrészt pedig a fogadó fél nyilvános kulcsát, és ezeket hozzáilleszti az érme végéhez. Így az érmét fogadó fél az aláírások ellenőrzésével ellenőrizheti az érme egymást követő tulajdonosainak láncolatát is.
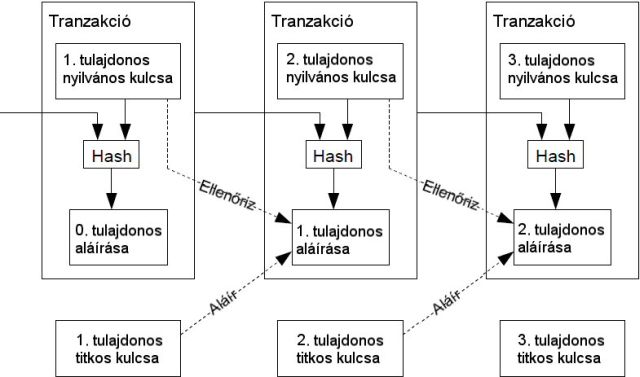Így azonban azt még nem tudja ellenőrizni az érmét fogadó fél, hogy a korábbi tulajdonosok egyike nem költötte-e el többször is a kérdéses érmét. Erre a problémára a bizalmas központi hatóság, avagy egy pénzverde bevezetése a leggyakoribb válasz, amely többszöri elköltések után kutatva ellenőriz minden egyes tranzakciót. Ez esetben minden tranzakció után vissza kell adni minden egyes érmét a pénzverdének, amely aztán újakat bocsát ki helyettük – így tehát csakis a közvetlenül a pénzverdéből érkező érmék esetében lehet biztos benne az ember, hogy azok nem lettek többször elköltve. Ezzel a megoldással csak az a baj, hogy a teljes pénzrendszer sorsa a pénzverdét üzemeltető vállalaton áll vagy bukik, mivel minden egyes tranzakciónak éppúgy keresztül kell mennie rajtuk, ahogyan a bankok esetében is.

Olyan megoldásra van tehát szükség, melynek segítségével az érmét fogadó fél megbizonyosodhat afelől, hogy a korábbi tulajdonsok nem írtak-e alá korábbi tranzakciókat. Esetünkben mindig csak az első – a legkorábbi – tranzakció számít, így a többszöri elköltésre irányuló későbbi próbálkozások már nem lényegesek. A korábbi tranzakciók hiánya felől pedig csak úgy bizonyosodhatunk meg, ha látjuk az összes tranzakciót. A pénzverde-alapú modellben egyedül a pénzverde látta át az összes tranzakciót, és így értelemszerűen az is döntötte el, hogy melyik érkezett be elsőként. Ahhoz, hogy bizalmas harmadik fél nélkül is elvégezhessük ugyanezt az ellenőrzést, egyrészt minden tranzakciót nyilvánosan be kell jelenteni [1], másrészt pedig ki kell alakítani egy olyan rendszert, melynek keretein belül a résztvevők közmegegyezésre juthatnak az egymást követő tranzakciók lezajlásának egyetlen, valós sorrendjéről. Bármely adott tranzakció esetében szükség van egy, a fogadó fél számára is elfogadható bizonyítékra arról, hogy a tranzakció elindításának időpontjában a csomópontok többségének közmegegyezése szerint is valóban az volt az első.

3. Időbélyegző szerver

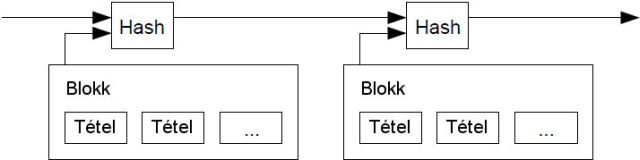
Ajánlott megoldásunk egy időbélyegző szerverrel kezdődik. Az időbélyegző szerver lényege abban áll, hogy széles körben nyilvánosságra hozza egy sor tételt magában foglaló blokk hashét, hasonlóan például egy újságban való leközléshez vagy egy Usenet poszthoz [2-5]. Az időbélyeg bizonyítja, hogy a kérdéses adatnak ekkor már – értelemszerűen – léteznie kellett ahhoz, hogy bekerülhessen a hashbe. Mindegyik időbélyeg hashe magában foglalja az előző időbélyeget is, hosszú láncot alkotva így, melynek minden újabb időbélyege megerősíti az előtte felhalmozódottakat.

4. Munkabizonyíték

Egy elosztott, P2P-alapú időbélyegző szerver kialakításához újság vagy Usenet-posztok helyett egy, Adam Back Hashcash-éhez [6] hasonló munkabizonyíték-rendszerre lesz szükségünk. Ennek lényege egy olyan érték előkeresése, amelynek a (például SHA-256-tal) előállított hashe egy bizonyos számú nullás bittel kezdődik. Az ehhez szükséges munkavégzés átlagos mennyisége a szükséges nullás bitek számával arányosan, exponenciálisan növelhető. A munka eredménye pedig egyetlen szimpla hashseléssel ellenőrizhető.

Az időbélyegző hálózatunkat tehát kiegészítjük egy olyan munkabizonyító rendszerrel, mely egy ún. nonce-értéket helyez el az egyes blokkokban. Ez az érték addig növelhető, amíg el nem ér egy olyan szintet, amelynek eredményeképp a blokk hashe a kívánt mennyiségű nullával kezdődhet. Ha ez a munkabizonyító számítási feladat egyszer már kielégítően elvégeztetett, akkor az így elkészült blokkot utólag nem lehet megváltoztatni anélkül, hogy az egész munkát újra meg ne kellene ismételni rajta. Ahogyan pedig egyre újabb blokkok kapcsolódnak mögé, úgy gyarapodik a szükséges munkamennyiség is, mivel egy adott blokk utólagos módosításához az utána következőket is mind újra kellene számítani.
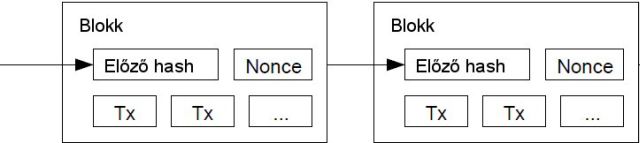A munkabizonyíték egyben megoldja a többségi döntéshozatalban való képviselet meghatározásának problémáját is. Ha egy-IP-cím-egy-szavazat-alapon határzonánk meg a többséget, akkor azon könnyen felülkerekedhetne bárki, aki elég sok IP-címet tud kiosztani. A munkabizonyíték azonban egy-számítókapacitás-egy-szavazat-alapú. A többségi döntéshozatalt a legnagyobb munkabizonyíték-erőfeszítést magában foglaló leghosszabb lánc képviseli. Ha a hálózat számítókapacitásának többségét tisztességes csomópontok adják, akkor a tisztességes lánc is fog a leggyorsabban bővülni, lehagyva minden más, vele esetlegesen versengő láncot. Egy korábbi blokk módosításához bármely támadónak nem csak hogy újra el kellene végeznie annak és az az után következő összes többi blokknak a munkabizonyíték-feladatát is, de ezután még fel is kellene zárkóznia a tisztességes csomópontokhoz, majd pedig le is kellene hagynia azokat. A későbbiekben azt is megmutatjuk, hogy egy lassabb támadó felzárkózásának esélye a lánchoz kapcsolt minden egyes újabb blokkal exponenciálisan csökken.

A gyorsuló hardverek és a csomópontok működtetése iránti érdeklődés időbeli változékonyságának kompenzálása érdekében a munkabizonyíték nehézségét egy mozgó átlaggal határozzuk meg úgy, hogy mindig biztosíthassuk az átlagos óránkénti blokkmennyiség állandóságát. Ha túl gyorsan generálódik túl sok blokk, akkor ezzel arányosan emelkedik a nehézség is.

5. Hálózat

A hálózat üzemeltetésének lépései sorban a következők:

1) Az új tranzakciókat bejelentik az összes csomópontnak.
2) Minden csomópont blokkba gyűjti az új tranzakciókat.
3) Mindegyik csomópont nekilát a blokkjához tartozó, adott nehézségű munkabizonyíték előkereséséhez.
4) Amint egy csomópont megtalál egy munkabizonyítékot, azonnal szétküldi a blokkját az összes többinek.
5) Azok az új blokkot csak akkor fogadják el, ha az abban foglalt valamennyi tranzakció érvényes, és nem tartalmaz többszöri elköltéseket.
6) A blokk elfogadását a csomópontok azzal jelzik, hogy átveszik az elfogadott blokk hashét, és azzal – mint előző hashsel – kezdenek dolgozni a lánc következő blokkján.

A csomópontok mindig a leghosszabb láncot fogadják el helyesnek, és azt bővítik tovább. Ha két csomópont egyidőben küldi szét a következő blokk két különböző verzióját, úgy egyesekhez értelemszerűen az egyik, másokhoz pedig a másik jut el előbb. Ebben az esetben mindegyik az elsőként beérkezettel dolgozik tovább, de az előző láncot is elmentik arra az esetre, ha az hosszabbra nőne. Ez a patthelyzet akkor törik meg, ha az egyik ágat egy újabb munkabizonyíték hosszabbra nyújtja a másiknál; ekkor az addig a másikon dolgozó csomópontok is átváltanak a hosszabb ágra, és azon dolgoznak tovább.

Nem kell feltétlenül eljutnia minden egyes újabb tranzakciónak minden csomóponthoz. Ha elég sok csomóponthoz jut el, akkor úgyis hamar bekerül egy blokkba. A blokk-küldés ezzel együtt toleráns is; ha egy csomópont nem kap meg egy blokkot, akkor a következő blokk fogadásakor észre fogja venni, hogy egyet kihagyott, és lekéri a hiányzót is.

6. Ösztönzés

Az új blokkok első tranzakciója megegyezés szerint egy speciális tranzakció, ami egy új érmét hoz a hálózatba, a blokk megalkotójának tulajdonaként. Ez szolgáltatja az ösztönzést a hálózatot fenntartó csomópontok működtetéséhez – egyrészt, másrészt pedig központi kibocsátó hatóság híján ez gondoskodik az új érmék forgalomba hozataláról is. Ez a folyamat párhuzamba állítható az aranyásók munkájával, akik saját erőforrásaik befektetésével dolgoznak új aranyrögök forgalomba hozatalán. Esetünkben a felhasznált elektromosság és számítókapacitás a befektetett erőforrás.

Ösztönzést jelentenek továbbá a tranzakciós díjak is. Ha egy tranzakció kimeneti értéke alacsonyabb a bemeneti értékénél, akkor a kettő közti különbség tranzakciós díjként hozzáadódik a tranzakciót tartalmazó blokk ösztönző értékéhez. Amikor már forgalomba került egy bizonyos, előre meghatározott mennyiségű érme, a tranzakciós díjak egyedüli és kizárólagos ösztönző erővé válhatnak, a rendszer pedig tökéletesen inflációmentessé.

Ez egyben őszinteségre is ösztönzi a csomópontokat. Ha egy kapzsi támadó valahogyan több számítókapacitást gyűjtene össze, mint amennyit az összes többi tisztességes csomópont együtt kitesz, akkor választania kell a már kifizetett pénze visszaszerzése vagy az új érmék generálása között. Még ez esetben is nyereségesebbnek bizonyulhat számára a szabályok – a mindenki másnál több új érme tulajdonosát előnyben részesítő szabályok – betartása, mint a saját gazdagsága alapjainak aláásása.

7. Tárhely-takarékosság

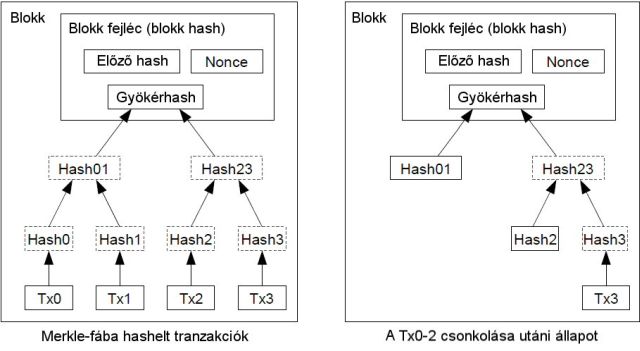
Ha egy érme legutóbbi tranzakcióját már elég sok újabb blokk temette maga alá, akkor az azt megelőző tranzakciói törölhetőek tárhely-takarékosság címén. Ahhoz, hogy ezt a blokk hashének megtörése nélkül kivitelezhessük, a tranzakciókat Merkle-fába [7][2][5] hasheljük, melynek csak a gyökerét hagyjuk benne a blokk hashében. A régi blokkok így tömöríthetőek a fa ágainak csonkolásával. A közbenső hasheket nem kell tovább tárolni.
Egy egyetlen tranzakciót sem tartalmazó blokk fejléc megközelítőleg 80 byte méretű lenne. 10 percenként egy újabb blokkal számolva 80 * 6 * 24 * 365 = 4,2 MB/év. Tekintve, hogy 2008-ban egy átlagos új számítógépet 2 GB RAMmal árulnak, Moore törvénye pedig 1,2 GB-os éves növekedést vetít előre, ezen adatok rögzítése még akkor sem okozhat gondot, ha a blokk fejléceket a memóriában is kell tárolni.

8. Egyszerűsített fizetésellenőrzés

A fizetések komplett hálózati csomópont üzemeltetése nélkül is ellenőrizhetőek. A felhasználónak ehhez csak a leghosszabb munkabizonyíték-lánc blokk fejléceinek egy példányára van szüksége, amihez pedig könnyen hozzájuthat a hálózati csomópontoktól. Amint megbizonyosodott róla, hogy valóban a leghosszabb láncot szerezte meg, megkaphatja a kérdéses tranzakciót az időbélyegzett blokkjához kapcsoló Merkle-ágat is. Magát a tranzakciót nem ellenőrizheti ugyan, de az ágnak a lánc megfelelő helyére való illesztésével arról így is megbizonyosodhat, hogy azt valóban elfogadta egy hálózati csomópontot, és hogy az utána következő újabb blokkok is megerősítik, hogy az egész hálózat is elfogadta.
Az ellenőrzés így mindaddig megbízható, amíg a hálózatot a tisztességes csomópontok uralják – sebezhetővé csak akkor válik, ha egy támadó legyőzi a hálózatot. Mert bár a csomópontok maguk is ellenőrizhetik a tranzakciókat, az egyszerűsített módszert alkalmazó felhasználókat a támadó mindaddig átverheti a hamis tranzakcióival, amíg fenn tudja tartani az uralmát a hálózat felett. Ezt például úgy lehetne kivédeni, ha a csomópontok riadóztatnák a hálózatot, ha érvénytelen blokkot észlelnek, felkérve a felhasználó kliensét a teljes blokk és a gyanús tranzakciók letöltésére a rendellenesség megerősítése érdekében. Persze a fizetéseket gyakran fogadó üzletek nagy valószínűséggel még így is szeretnének majd saját csomópontot működtetni a biztonságuk függetlenítése és a minél gyorsabb ellenőrzés érdekében.

9. Osztás és egyesítés

Lehetne ugyan egyedileg is kezelni az egyes érméket, de felettébb célszerűtlen lenne minden egyes utalás minden egyes centjét külön tranzakcióként jegyezni. Ezért, az oszthatóság és egyesíthetőség érdekében az egyes tranzakcióknak több bemenetük és több kimenetük is lehet. Rendes körülmények között vagy csak egy nagyobb, előző tranzakcióból származó, vagy pedig több, kisebb utalások összegeit egyesítő bemenet lesz, kimenetből pedig legfeljebb kettő: maga a kifizetett összeg és az esetleges visszajáró a feladónak.
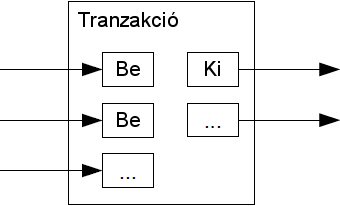Megjegyzendő, hogy ez a sokszoros elágazás (vagyis hogy egy tranzakció több másikon alapul, és azok is még több másikon, stb.) itt nem jelent problémát, mivel soha nincs szükség egy bizonyos tranzakció összetevői előéletének teljes és részletekbe menő feltárására.

10. Adatvédelem

A hagyományos banki modell valamennyire biztosítja az adatok védelmét azáltal, hogy korlátozza az azokhoz való hozzáférést úgy a tranzakció résztvevői, mint a bizalmas harmadik fél számára is. A tranzakciók nyilvános bejelentésének szükségessége ezt nem teszi lehetővé – azonban az adatok kiszivárgását másképp is megakadályozhatjuk, jelesül a nyilvános kulcsok névtelenségének megőrzésével. Azt bárki láthatja, hogy valaki épp küldött egy bizonyos összeget valaki másnak, de konkrét személyekhez ezt már nem tudja kötni. Ez a tőzsdék adatkezelésével állítható párhuzamba, ahol szintén nyilvánosságra hozzák az egyes adásvételek időpontját és volumenét (a “szalagot”), de azt már nem, hogy melyikben kik voltak érintettek.
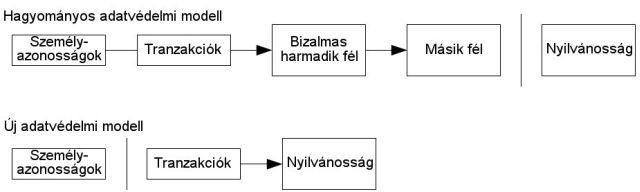Másodlagos tűzfalként érdemes minden tranzakcióhoz új kulcspárt használni, hogy semmiképp se köthesse össze őket senki illetéktelen valós személyekkel. Valamennyi kockázat azonban így is marad a több-bemenetes tranzakciók esetében, mivel ezek szükségszerűen felfedik, hogy a bemeneteik egyazon tulajdonostól származnak. Ha pedig ismertté válik egy kulcs tulajdonosa, akkor azon keresztül az érintett tulajdonos más tranzakcióihoz is el lehet jutni.

11. Számítások

Vegyük most fontolóra azt az esetet, amikor egy támadó megpróbál gyorsabban generálni egy saját láncot, mint ahogyan a tisztességes csomópontok bővítik az eredetit. Még ha sikerrel is járna, a rendszer akkor sem nyílna meg az önkényes változtatások – így például a semmiből teremtett vagy a támadóhoz soha nem tartozott pénz elvétele – előtt, mivel a csomópontok nem fogadnak el sem érvénytelen tranzakciót fizetségképp, sem pedig ilyeneket tartalmazó blokkokat egyáltalán. A támadó csak a saját korábbi tranzakcióinak megváltoztatásával próbálhatja meg visszaszerezni az egyszer már kiadott pénzét.

A tisztességes és a támadó lánc versengését binomiális véletlen sétaként jellemezhetjük. Siker-esemény az, ha a tisztességes lánc bővül egy újabb blokkal (+1 előny), kudarc-esemény pedig az, ha a támadó lánc bővül egy újabb blokkal (-1 előny).

Annak az esélye, hogy egy támadó lánc behozzon egy adott mértékű lemaradást, a játékos csődjének problémájával állítható párhuzamba – amikor is feltesszük, hogy egy korlátlan hitelkerettel rendelkező szerencsejátékos mínuszból indulva, potenciálisan végtelen számú játszmával próbálja nullszaldóra feltornászni az egyenlegét. Annak a valószínűségét, hogy elérheti-e valaha is a nullszaldót – vagy hogy egy támadó valaha is felzárkózhat-e a tisztességes lánchoz -, a következőképpen számíthatjuk ki [8]:

p = annak a valószínűsége, hogy egy tisztességes csomópont találja meg a következő blokkot
q = annak a valószínűsége, hogy a támadó találja meg a következő blokkot
qz = annak a valószínűsége, hogy a támadó valaha is felzárkózhat z blokk hátrányból
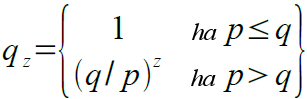Kiindulva azon előfeltevésünkből, miszerint p > q, a felzárkózás esélyét exponenciálisan csökkenti minden egyes újabb, a támadó lemaradását növelő blokk. Mivel az esélyek ellene szólnak, ezért ha nem sikerül szerencsésen előrelendülnie még a kezdet kezdetén, akkor annál jelentéktelenebbé válnak az esélyei, minél jobban lemarad.

Lássuk, mennyi időnek kell eltelnie ahhoz, hogy egy tranzakció fogadója kellőképpen megbizonyosodhasson arról, hogy a feladó már nem fordíthatja vissza a tranzakciót. Jelen esetben feltételezzük, hogy a feladó egy támadó, aki egy ideig el akarja hitetni a fogadóval, hogy valóban fizetett neki, majd visszafordítaná az utalást, hogy visszaszerezze a pénzét. Ez esetben a fogadó fél riasztva lesz ugyan, de a támadó bízik benne, hogy akkor már késő lesz.

A fogadó tehát generál egy új kulcspárt, és csak az aláírás előtt nem sokkal adja meg a nyilvános kulcsot a feladónak, elejét véve így annak, hogy az – bízva a szerencséjében – már előre elkezdhesse a blokkgyártást, és épp a megfelelő pillanatban hajthassa végre a tranzakciót. Amint a tranzakció elküldésre került, a csaló titokban nekilát a saját, párhuzamos blokklánca bővítésének, amelyben már módosította ezt a legutóbbi tranzakcióját.

A fogadó addig vár, amíg a tranzakció bekerül egy blokkba, és még z újabb blokkot is fűz fel utána a láncra a hálózat. Nem tudja ugyan, hogy a támadó ez idő alatt mennyit haladt, de feltételezve, hogy a tisztességes blokkok az elvárt átlagos ütemben bővülnek, a támadó potenciális haladását elvárt értékes Poisson-eloszlással számolhatjuk ki:
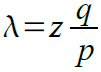Annak valószínűségét, hogy a támadó innen még felzárkózhat-e, úgy kaphatjuk meg, ha megszorozzuk a lehetséges haladását az adott ponttól való felzárkózásának valószínűségével:
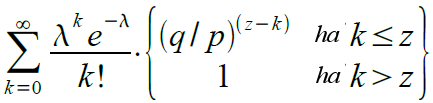Az eloszlás végtelen farkának összegzését elkerülendően átrendezve:
C kóddá konvertálva…

#include double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 – q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k {
double poisson = exp(-lambda);
for (i = 1; i poisson *= lambda / i;
sum -= poisson * (1 – pow(q / p, z – k));
}
return sum;
}

Ezt különböző értékekkel lefuttatva láthatjuk, hogy z növekedésével exponenciálisan csökken a felzárkózás valószínűsége.

q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012

q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006

Megoldás 0,1%-nál alacsonyabb P-vel…

P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340

12. Összefoglalás

Egy olyan elektronikus tranzakció-kezelő rendszert vázoltunk fel, melyhez nincs szükség bizalomra. Digitális aláírásokból összeállított érmék szokványos keretrendszeréből indultunk ki, melyek garantálják ugyan a tulajdonlás biztonságát, ám önmagukban nem elégségesek egy, a többszörös elköltést megakadályozó rendszer nélkül. Ezért vázoltunk fel egy, a tranzakciók nyilvános történetét munkabizonyítékkal feljegyző P2P-hálózatot, melynek mindaddig nem célszerű a megtámadása, amíg tisztességes csomópontok adják az összesített számítókapacitás többségét. A hálózat erős a maga strukturálatlan egyszerűségében. A csomópontok egyszerre, minimális koordinációval dolgoznak. Nem kell azonosítani őket, mivel az üzeneteknek nincs konkrét címzettjük, és elég csak a lehető legtöbb helyre eljutniuk. A csomópontok tetszés szerint hagyhatják el a hálózatot és térhetnek vissza, elfogadva a munkabizonyíték-láncolatot a távollétükben történt események tanúságaként. A számítókapacitásukkal szavaznak, tovább-bővítéssel fogadva el az érvényes blokkokat és tovább nem bővítéssel utasítva el az érvényteleneket. Ezzel a közmegegyezéses rendszerrel minden szükséges szabály és ösztönzés bevezethető és életbe léptethető.

Hivatkozások

[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila és J.-J. Quisquater, “Design of a secure timestamping service with minimal trust requirements”, 20th Symposium on Information Theory in the Benelux, 1999. május.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document”, Journal of Cryptology, 3. kötet, 2. szám, 99-111. old., 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping”, Sequences II: Methods in Communication, Security and Computer Science, 329-334. old., 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings”, Proceedings of the 4th ACM Conference on Computer and Communications Security, 28-35. old., 1997. április.
[6] A. Back, “Hashcash – a denial of service counter-measure”, http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems”, Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, 122-133. old., 1980. április.
[8] W. Feller, “An introduction to probability theory and its applications”, 1957.

Forrás: Bitcoin